word problems – Astute Hoot

Strengthen Mathematical Understanding in 4 Easy Steps

February 17, 2016February 17, 2016By astutehoot

Mathematical understanding means that students understand the story problem and follow the problem-solving steps. Understanding story problems can be very challenging because it requires multi-step, higher-level thinking processes. Students are required to process several pieces of information before starting any mathematical operations. If students do not understand the problem, they will solve it incorrectly, even if they have a strong repertoire of strategies. Strengthen your students’ mathematical understanding with these 4 easy steps:

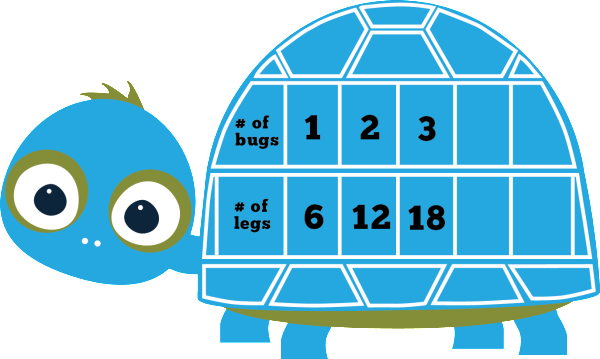
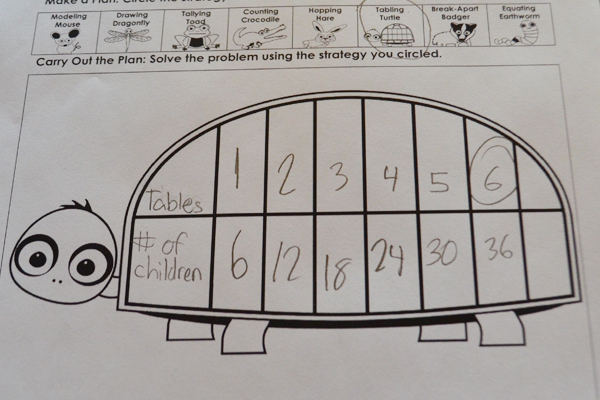
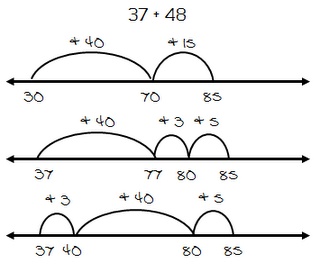
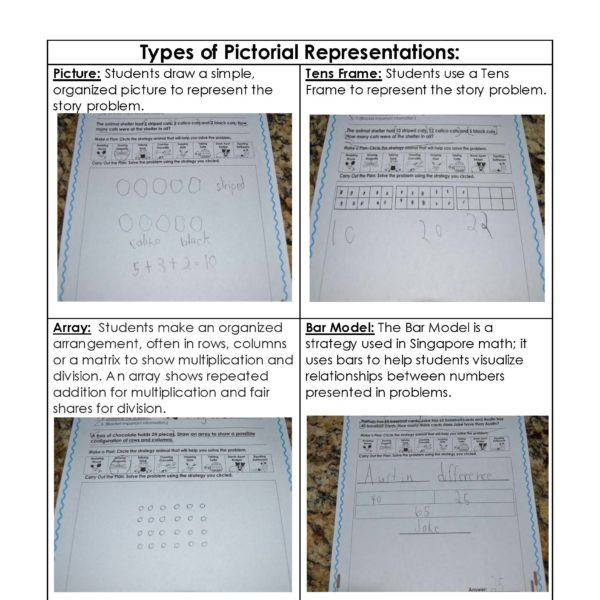
1. Scaffold instruction: Mathematical understanding includes many steps: identify question; identify key information; get rid of erroneous information; determine the operation; solve using an appropriate, efficient strategy. Since mathematical understanding involves so many steps, teachers should teach each step explicitly and introduce the next step after proficiency is demonstrated. This allows the teacher to isolate individual steps first and then gradually integrate the steps together.

2. Incorporate multi-sensory activities: Allow students to act out the problem and use manipulatives to help students build understanding. In my classroom, students use Upton Understanding Fish to help them complete the problem-solving steps. I purchased a inexpensive, yellow Webkinz fish from Ebay to use as our classroom Upton.

During direct instruction, I model each of the problem-solving steps, thinking aloud as I go. I hold Upton right beside me and will often talk to him during my think-alouds. The students think it is funny, but it keeps them engaged. During guided practice, I toss Upton to different students, asking them to help me complete one of the problem-solving steps. Students also take turns using Upton to assist during independent problem-solving time.

Reading with Upton 2

The stuffed Upton fish has become a pivotal piece of my problem-solving instruction because it helps kids feel safe to take risks and discuss problem-solving steps. In fact, a few of my students have even asked their parents for their own Upton as a birthday or Christmas gift.

3. Use discussion questions and prompts:Students are more successful at solving math problems when they monitor and reflect upon their thinking and problem-solving steps as they work through problems. We often assume that students know how to thoroughly discuss their mathematical thinking and problem-solving steps, but like an other concept or skill, this must be taught in depth. Teachers must model the self-questioning process and provide multiple opportunities and support for students to practice it until they can use the questioning strategies independently.

I use Upton’s self-reflection questions and peer discussion prompts to facilitate mathematical discussion. I introduce one prompt or question at a time and add additional prompts in subsequent lessons.

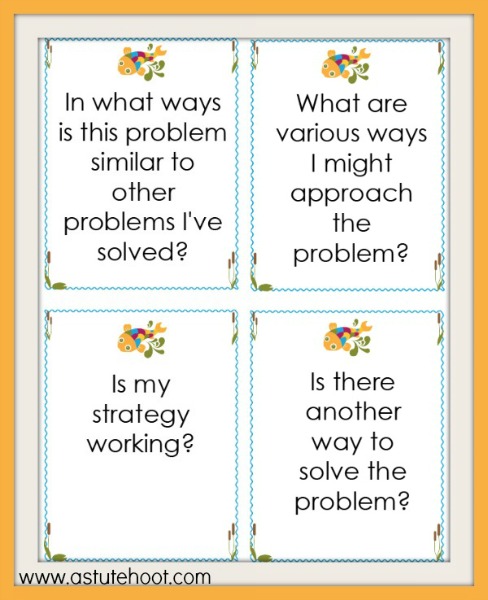
MathProblemSolvingSelfReflectionandPeerDiscussionQuestions.pdf-6 (2)

During lunch (before our problem-solving time), I leave the new prompt or question right by Upton as if he is presenting it to the class. When I pick the kids up for lunch, I tell them that Upton left us something and they get so excited to read his new question or prompt.

4. Provide anchor charts: Post the problem-solving steps in a prominent place in classroom. I add a visual cue for each step to promote understanding. As you teach problem-solving, refer to these posted steps and encourage students to do so when solving independently as well.

Download our Upton Understanding Fish problem-solving unit and accompanying self-reflection and peer discussion questions and prompts to help build mathematical understanding in your classroom.

Jessica_blog_signature-SMALL

Create Write-On, Wipe-Off Problem-Solving Journals

January 3, 2016By astutehoot

Problem-solving plays an important role in my daily math instruction. Students use pre-made journals to help them complete the problem-solving steps, solve the problem in 2 ways, explain their thinking and rate themselves on a learning scale. These journals track students’ progress with mathematical understanding, strategy selection and application. They also serve as an effective assessment tool. I decided to make a write-on, wipe-off version for students to use during math centers. Follow these 4 easy steps to make them for your classroom, too!

1. Gather materials: You will need a class set of manila folders, problem-solving journal templates, glue sticks, a laminator and dry erase markers.

2. Prepare folders: Glue on the front cover, problem-solving pages on the inside, and the discussion prompts on the back. Laminate and cut out (a perfect job for a parent volunteer).

Journal front 1.5 Inside of problem solving journal Back of problem solving journal mat

3. Select appropriate story problems: I use differentiated story problems during math instruction and color code to keep them organized. An extensive story problem bank is included in our Problem-Solving Essentials Bundle.
Word problems

4. Model procedures and provide practice: Explain how to use the write-on, wipe-off problem-solving journals. Model how to use a dry erase marker to complete the journal. Select a partner to use the discussion prompts, thinking aloud as you go. Practice using the journals during whole group instruction, roving to monitor student understanding. As students demonstrate understanding, incorporate these journals into math center time, either at an adult-led center or an independent math center.

Page 1.5 Inside of journal

Download our Math Intervention Problem-Solving Essentials Bundle for over 200 pages of lessons, activities, worksheets, printables, everything you need for comprehensive problem-solving instruction during math intervention, special education and general education.

Jessica_blog_signature-SMALL

Emmy Equating Earthworm Is Here!

April 20, 2014March 20, 2015By astutehoot

Emmy Equating Earthworm here.
I help you write a variety of equations without any fear.
Horizontally or vertically, it doesn’t matter the direction,
I will help you solve each one to numerical perfection.

Emmy Equating Earthworm is our newest animal in our Problem-Solving Pond: A Common Core Math Strategy Unit. The Problem-Solving Pond was created to help teachers overcome Common Core math challenges and employ problem-solving strategies with confidence and fidelity. Emmy’s unit is perfect for general education, special education, RTI and math intervention. Read more about Emmy’s strategy below or download the complete unit here.

WHAT is an equation? Students write an equation, or number sentence to solve a story problem or show their work after using another method (e.g., drawing a picture, using manipulatives, making a table, etc.). Solving equations is the very beginning of being able to do algebra. The basic idea behind solving equations is to be able to find the missing number. Students can use a variety of strategies to solve equations, including traditional algorithms. Traditional algorithms involve repeating a series of steps over and over as in carrying in addition and borrowing in regrouping.

WHY are equations important? Traditional algorithms have been the core of many elementary mathematics programs for years as educators focused on quick, precise calculations and paper-pencil drill. Math instruction has drastically changed the last few years with the implementation of Common Core State Standards and the heavy emphasis on science and math instruction. Students are now required to solve real-world math problems using a variety of strategies while explaining thinking and justifying solutions.

Traditional algorithms, or equations, are still acceptable to use as secondary strategies to double-check work and to summarize the mathematics behind the problem-solving process.

HOW do I teach equations? The first major step is to teach students how to find a missing number. This means that students need to be familiar with their basic facts first. Practice a variety of ways to find the missing number using many different equations. Next, teach addition and subtraction without regrouping; once proficiency is demonstrated, introduce regrouping.

WHEN should I introduce equations? Basic equations and number sentences should be introduced when you begin teaching the problem solving process. This is also an ideal strategy for proficient mathematicians who have a strong number sense foundation, fluency with basic facts, and are able to quickly conceptualize a problem and use a traditional algorithm to solve. It is most effective to introduce traditional algorithms after students are able to regroup numbers using place value manipulatives. It is critical that students understand and can articulate the regrouping process before using a traditional algorithm.

Helpful hints:

Model writing equations and number sentences. Regularly model using think-alouds to demonstrate how equations are used as part of the problem-solving process. Be explicit in your models to show students how equations can also be used to check their work after using a different strategy to solve the problem.

Provide place value and equation building practice. Students need a strong place value foundation to use traditional algorithms effectively. Provide regular practice through center games and kinesthetic activities. Simple games such as “Race to 100” where students roll dice and add numbers using place value manipulatives are engaging and effective. Incorporate equation building activities into weekly center rotations as well.

Use visual support. Use the following Subtraction Poem to reinforce regrouping. Place value and regrouping posters are also helpful tools to post while students are using the traditional algorithm method.

It’s Tom Tabling Turtle!

April 13, 2014March 20, 2015By astutehoot

Howdy, I’m Tom Tabling Turtle and I make tables-
These are columns and rows with numbers and labels.
Always organize your information, is what I say,
So you can discover patterns and relationships in a logical way.

Tom Tabling Turtle is our newest animal in our Problem-Solving Pond: A Common Core Math Strategy Unit. The Problem-Solving Pond was created to help teachers overcome Common Core math challenges and employ problem-solving strategies with confidence and fidelity. Tom’s unit is perfect for general education, special education, RTI and math intervention. Read more about Tom’s strategy below or download the complete unit here.

WHAT is the table strategy? Students make a table complete with labeled columns and rows. The table strategy helps students write information in an organized format, allowing them to easily identify number patterns and relationships.

WHY is the table strategy important? When students make a table, they organize information in a logical way and critically examine data patterns to create a solution.

HOW do I teach the table strategy? When you introduce and practice the strategy, give students a pre-made table. Todd’s turtle shell provides scaffolding with space for labels and organized columns and rows for neat data entry. As students become proficient with the table strategy, teach them to make their own table so they can use this strategy independently without the need for a pre-made table.

WHEN should I use the table strategy? This is an ideal strategy for developing mathematicians who have a solid number sense foundation. It is most effective for repeated addition or multiplication story problems.

Helpful hints:

Use a pre-made table. Young students often lack fine motor skills needed to construct a table, but are perfectly capable of using this strategy. Provide a pre-made table, such as Tom’s turtle shell or a simple table made in Microsoft Word so students can easily input data.

Provide visual support. After teaching students how to construct a table, be sure to write and post directions (along with visual support) in a prominent place during problem-solving time. Students would also benefit from an anchor chart like this one as well.

Say Hello to Hailey Hopping Hare

March 23, 2014March 20, 2015By astutehoot

I’m Hailey the Hopping Hare, I’m the skip-counting master.
This is a skill that helps to count things faster;
Learn to count up or down by a number other than one.
Quick like a bunny, you soon will be done.
Keep in mind that skip counting is repeated addition.
Moving swiftly through problems is my main mission.

WHAT is hopping? Students use place value and number sense to add or subtract numbers. Students first start with the bigger number in the problem; this number is the starting point for hopping. Then they decompose or break apart the second number by place value (into 10’s and 1’s). Depending on the problem, students will either add or subtract, hopping first by 10’s and then by 1’s. Students label numbers above hops to help ensure solution is correct. Read more about Hailey’s strategy below or download the complete unit here.

WHY is hopping important? When students use the hopping strategy, they are essentially skip-counting by 10’s and 1’s. This helps strengthen mental computation, builds number sense and solidifies foundational place value skills. It also serves as an efficient method for students to double-check solutions. Furthermore, hopping can easily be extended to larger numbers and multi-step problems because it tracks mathematical thinking and steps taken to complete problem.

HOW do I teach hopping? Teach hopping in isolation first so that students become familiar with the process of identifying larger number and decomposing smaller number by place value. Use patterned, pre-labeled or open number lines until students can proficiently count and track hops (see examples). After proficiency is demonstrated, introduce an open number line where students determine the starting point then draw and label hops without support.

WHEN should I use hopping? This is an ideal strategy for developing mathematicians who have a solid place value and number sense foundation. It is most effective to introduce the hopping strategy after students become proficient with the counting strategy. When larger numbers are used, students quickly realize that counting becomes inefficient and laborious. Hopping allows students to employ counting skills they are comfortable with, but increases rigor and mathematical practice.

Helpful hints:

Supply models and provide kinesthetic practice. Select appropriate number lines according to students’ individual needs. Some students will easily grasp hopping and will be able to use the open number line while others will need the patterned number line to see and count the 10’s and 1’s. Make a large patterned number line for kinesthetic learners and have them physically hop the numbers. Students will not only love this activity, the multi-modal approach reinforces learning.

Make Hailey pointers. Cut out and laminate Hailey patterns and use a hot glue gun to adhere to craft sticks. Students can use a Hailey pointer to hop the numbers in each problem.

Practice skip-counting. Some students struggle with skip counting and could benefit from repeated practice. Chanting by 100’s, 10’s and 1’s while walking in line, calendar time, even clean-up time all serve as great practice opportunities. Be sure to vary starting points so to ensure that students aren’t just counting by multiples of 100’s, 10’s or 5’s. (For example start at 57 and count by 10’s, then switch and count by 1’s.)

Be flexible with students’ hopping methods. Remember, the whole point of teaching strategies is to help students become fluid, flexible thinkers with deep conceptual understanding. While Hailey teaches students to start with bigger number and hop by 10’s and then 1’s, do not insist that students need to only hop this way. It is imperative to allow them to experiment and try multiple methods in order to find the most meaningful and efficient hopping method for themselves. Some hop to the nearest multiple of 10 and then continue hopping by 10’s, while others hop by all of the 10’s in one hop. Accept all methods if students solve problem correctly, explain method and apply across settings.

Introducing Daphne Drawing Dragonfly

March 22, 2014March 20, 2015By astutehoot

Hi, I’m Daphne the Drawing Dragonfly.
Draw a mathematical picture to give my strategy a try.
Read the problem and draw what’s going on;
Then write a number sentence for what you have drawn.

Daphne Drawing Dragonfly is our newest animal in our Problem-Solving Pond: A Common Core Math Strategy Unit. The Problem-Solving Pond was created to help teachers overcome Common Core math challenges and employ problem-solving strategies with confidence and fidelity. Daphne’s unit is perfect for general education, special education, RTI and math intervention. Read more about Daphne’s strategy below or download the complete unit here.

WHAT is drawing? Students make a visual representation of the story problem such as a picture, bar model, tens frame or array.

WHY is drawing important? When students use the drawing strategy, they are making a concrete representation, strengthening understanding of the mathematical concepts. Effective math classrooms include frequent use of pictorial representations to help students process and visualize mathematical concepts learned.

HOW do I teach drawing?Teach students to create neat, organized drawings with labels and numbers. Students will need to be taught the bar model and arrays, but it is best to let students create the pictorial representation that they see and works for them.

WHEN should I use drawing? This strategy is ideal for presenting a new mathematical operation. Most teachers use this strategy with K-2 mathematicians, but this is also beneficial for older students as it works especially well with money, fractions, ratios and percentages. Drawing is a great way to double-check solutions because the visual representation increases understanding of the problem.

Helpful hints:

Create drawing guidelines. As a class, decide important components to include in a mathematical drawing. Possible components include:
- Simple drawings
- Appropriate spacing
- Neat labels (words or numbers)
- Easy to read

$Guidelines for math pictures$

Encourage students to use a variety of pictorial representations. Often students will get in a “strategy rut”, relying on one strategy for many different kinds of story problems. While drawing is an effective strategy for most problems, the type of pictorial representation used depends on the type of story problem.

Presenting Tallying Toad

March 13, 2014March 20, 2015By astutehoot

Hello, I’m Tallying Toad.
I get you started on the problem-solving road.
A tally mark is a straight line to show one;
Group tallies into five is how it’s done.
First make four tallies, nice and straight;
Then make a diagonal fifth tally and you’re doing great!

Todd Tallying Toad is our newest animal in our Problem-Solving Pond: A Common Core Math Strategy Unit. The Problem-Solving Pond was created to help teachers overcome Common Core math challenges and employ problem-solving strategies with confidence and fidelity. Read more about Todd’s strategy below or download the complete unit here.
WHAT is tallying? Students use tally marks to show the numbers represented in the story problem.

WHY is tallying important? When students use the tally strategy, they learn to count and notate groups of 5, strengthening number sense in the process. Tallying is an easy, quick way to double-check solutions for kindergarten and first-grade students.

HOW do I teach tallying? Teach tallies in isolation first so that students become proficient making neat, organized tally marks. After proficiency is demonstrated, introduce tallying as a problem-solving strategy and teach students to apply within a mathematical context.

WHEN should I use tallying? This is an ideal strategy for beginning mathematicians who are learning to count and record numbers. Tallying is a great way to represent smaller numbers in story problems. Students get comfortable with tallies and will try to apply to larger numbers, making some teachers cringe. Refrain from discouraging use of tallies for larger numbers; students must independently develop understanding that tallying is not an efficient, effective strategy for story problems with larger numbers.

Helpful hints:

• Supply models and provide kinesthetic practice. Beginning mathematicians often lack dexterous fine motor skills, which can impede formation of neat, straight tally marks. Provide craft sticks, Wikki Sticks or pipe-cleaners (cut in half) and have students make a model of the tallies before drawing them on paper. Allow students to practice kinesthetically in salt or Jell-o trays or trace on bumpy paper. Students can also practice making tallies with Play-Doh.

• Include visual support. As beginning mathematicians start to use tally strategy, they need visual support to ensure that tally marks are straight neatly organized into groups of 5.

• Practice counting by 5’s. Some students struggle with skip counting and could benefit from repeated practice. Chanting 5’s while walking in line, calendar time, even clean-up time all serve as opportunities for fun skip counting practice.

Introducing Clark Counting Crocodile

March 3, 2014March 20, 2015By astutehoot

I’m Clark the Counting Crocodile. Use me to help you count.
Start with the largest number, and draw lines for the remaining amount.
Count on for addition, count back for subtraction;
Then circle the answer as your final action.

Clark Counting Crocodile is the second strategy animal in our Problem-Solving Pond: A Common Core Math Strategy Unit. The Problem-Solving Pond was created to help teachers overcome Common Core math challenges and employ problem-solving strategies with confidence and fidelity. Read more about Clark’s strategy below or download the complete unit here.

WHAT is counting?As students build their number sense and fluency, they are able to solve a story problem with counting. In this strategy, students will learn to count on for addition and count back for subtraction using a 100’s chart for support as needed.

WHY is counting important?Counting is a crucial strategy because it helps students explore the relationships and patterns between numbers. Students need to recognize the order of numbers so they can understand that it is more efficient to start with bigger number. For example, in order to solve “4+27,” they should start counting from 27 and progress to “28, 29, 30, 31” instead of starting from 4 and progressing to 31, because in the latter case, they would have to count much more, increasing the possibility of errors. Proficient counting lays the foundation for number sense and place value.

HOW do I teach counting? Explain that Clark helps mathematicians solve problems by counting on to find the total or counting back to find the difference.

Counting on for addition: Students start with largest number in the problem; they put that number in Clark’s mouth and then draw the number of lines for the second number in the problem (if the second number is 14, students would draw 14 lines). Students then label the lines (below the line) and count on, writing each number above the line. Students circle the answer and write equation below to solidify understanding.

Counting back for subtraction: Students start with the largest number in the problem; they put that number in Clark’s mouth and then draw the number of lines for the second number in the problem (if the second number is 14, students would draw 14 lines). Students then label the lines (below the line) and count back, writing each number above the line. Students circle the answer and write equation below to solidify understanding.

WHEN should I use counting? This strategy isideal for problems that include smaller numbers. Most teachers use this strategy with K-2 mathematicians, but this is also beneficial for older students as it works for money, multiplication and division (included in unit).

Helpful Hints:

Create counting bags. Create counting bags with different numbers of objects in each bag and a set of appropriate number cards. Use common manipulatives such as cubes, beans, tiles for bags. Students also love seasonal items such as conversation hearts, acorns, pumpkins, shamrocks, etc. Have student count objects in each bag and then select the number card to name that amount. Students can simply place the objects and number card back into the baggie for checking. Mark the bags with letters or shapes for easy checking of student work.

Provide opportunities for strategy exploration. Allow students to build conceptual understanding by having them solve a counting problem in multiple ways. Students can solve the problem starting with the big number first and double-check solution by starting with the smaller number first. This exploration will guide students to recognize that while it is more efficient to start with the larger number in the problem, number order does not affect the sum. Provide templates with larger numbers; this will help students observe that the counting strategy is not efficient for larger numbers.