Set Up Your Best Classroom Yet: Part 2
Yesterday as part of my blog series, Set Up Your Best Classroom Yet, I gave you a sneak peek into my second grade classroom with a focus on my guided reading area. I use the district prescribed curricula along with our reading, writing, and math strategy animals to help my students learn, apply, and transfer critical strategies across settings. My classroom décor centers around Hazel Hoot, an adorable green screech owl, and her special strategy friends. See how I integrate the Problem-Solving Pond along with our hands-on tools to support and enhance the required Saxon math curricula.

Special Spaces
Problem Solving Pond
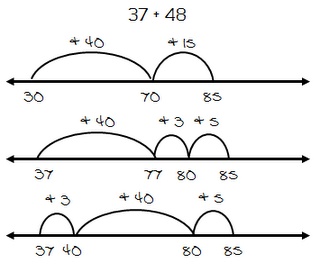
In our sequel, Hazel Meets the Math Strategy Friends, Hazel swoops down to catch her dinner at the local pond when she grabs Upton, an enchanted fish. Upton oversees Problem-Solving Pond and promises to introduce Hazel to his animal friends, all who teach a special problem-solving strategy. Using these strategies and Upton’s guidance, Hazel blossoms into an accomplished mathematician who is able to tackle problems with ease.

In order to recreate the Problem-Solving Pond, I covered a bulletin board with fadeless blue water paper and added green tulle and silk pond stems to border the pond. Upton’s Solving Word Problems Poster and Strategies Banners are prominent features of Problem-Solving Pond; I reference them throughout each lesson. I printed our Problem-Solving Pond Bulletin Board Set added Velcro to the back of each strategy animal allowing me to detach to use during lessons.

 I found this stuffed animal on Ebay that looks just like Upton and hung it with fishing wire and a plastic hook. During guided practice, I toss Upton to students and he helps us complete the problem-solving steps. Students LOVE solving problems with him!
I found this stuffed animal on Ebay that looks just like Upton and hung it with fishing wire and a plastic hook. During guided practice, I toss Upton to students and he helps us complete the problem-solving steps. Students LOVE solving problems with him!
 I also found inexpensive jars at Hobby Lobby to hold our hands-on tools such as Max’s Counters, Brian’s Slide and Learns, and Fiona’s Fact-Fluency Pencils and added these adorable labels.
I also found inexpensive jars at Hobby Lobby to hold our hands-on tools such as Max’s Counters, Brian’s Slide and Learns, and Fiona’s Fact-Fluency Pencils and added these adorable labels.
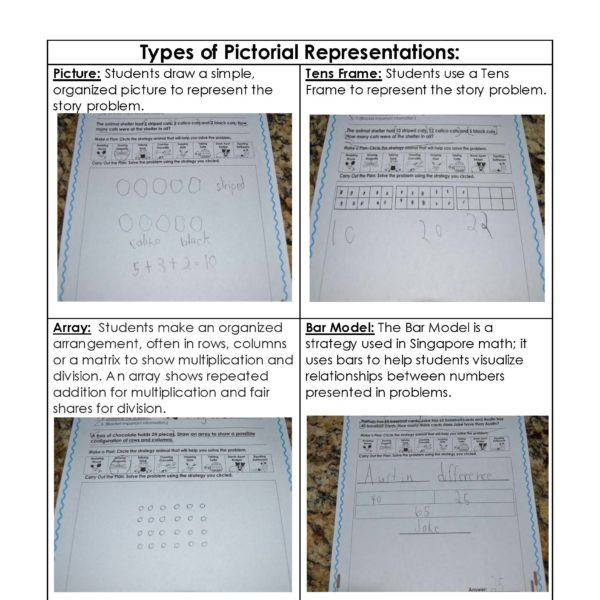
 During center time, students solve their Saxon story problems using the strategy animals and our Problem-Solving Journals. They also use our hands-on tools such as Problem-Solving Mats, Brian’s Slide and Learns and Fiona’s Fact-Fluency Flashcards to reinforce learned strategies and concepts.
During center time, students solve their Saxon story problems using the strategy animals and our Problem-Solving Journals. They also use our hands-on tools such as Problem-Solving Mats, Brian’s Slide and Learns and Fiona’s Fact-Fluency Flashcards to reinforce learned strategies and concepts.


Students enjoy using the Astute Hoot rug to discuss their journal samples. They stand on the strategy animal that they used to solve the story problem and then discuss the strategies, process, and thinking they used.
 Read tomorrow’s blog to see my Writing in the Wild West classroom space and accompanying hands-on tools.
Read tomorrow’s blog to see my Writing in the Wild West classroom space and accompanying hands-on tools.














 Finally, I made these adorable owl cupcakes and wrote a special note on the door as a hint to the big surprise.
Finally, I made these adorable owl cupcakes and wrote a special note on the door as a hint to the big surprise.